一応、MNISTについても触れておきます。MNISTとは、0~9の数字手書き画像のデータベースです。
(↓こんな感じ)
DLのテストでは、学習器がパターン認識で予測した数字と正解の数字を比べ、その正答率をパフォーマンス指標とします。LeCun教授(機械学習分野の第一人者)が管理しており、必要に応じて、ダウンロード可能です。
サンプルコードについて
CNN学習器の構造は、公式のTutorialを基に構築しています。haminikuさん(リンク先記事作成者様)が、それを統合しました。
わずかながら、個人的に改変したサンプルコード(mnist_expert.py)も、こちらに添付します。このファイルは、上記の統合ファイルに加えて、個人的に計測時間を確認できるように改良したものです。マシンの性能ベンチマークにも使えるかと思います。以下記事に引用するコードも全て添付のコードから抜粋しております。
参考ページ(Qiitaの記事)
1. 【TensorFlowのTutorialをざっくり日本語訳していく】2. Deep MNIST For Experts
2. TensorFlowチュートリアル - 熟練者のためのディープMNIST(翻訳)
3. TensorFlow 畳み込みニューラルネットワークで手書き認識率99.2%の分類器を構築
CNNのマップ
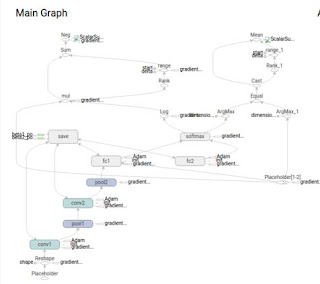
詳細コードに入る前に、このモデルの学習アルゴリズムを概観しておきます。天下り的ですが、全体図を下記に添付します。
この図は、TensorBoardというTensorFlowの可視化ツールから抽出することができます。
(1) 入力層
(28x28=)784次元のベクトルが入力ベクトルです。数字の画像を784ピクセルに分割し、1次元=1ピクセルで情報を代入しています。
(2) 畳込み層1→プーリング層1
2層準備。ゼロパディングという補完機能を利用しています。フィルタの畳込みに対して、周縁データが欠落するのですが、その補完のためにパディングを用います。(パディングの話で推測できるように、畳込み層では、入力の次元圧縮を行いません。)
プーリングでは、畳込みで返された数値を圧縮します。ここでは、最大プーリングという、最も基本的な手法を用いています。最大プーリングでは、設定範囲のピクセルの中で一番いいやつをピックアップします。プーリングでも、パディングを行うことがあります。(重ねあわせがずれる領域が存在することがあるため)
(3) 畳込み層2→プーリング層2
(2)の繰り返しでさらに圧縮→この段階で7 x 7 = 49次元まで落とす予定です。
(4)全結合層(高密度結合層)
抽出したプーリング層からの出力層を入力層に送り、NNのような処理をかけます。活性化関数はReLUです。
(5)クラス分類処理
ソフトマックス関数の計算→交差エントロピー誤差関数による評価
mnist_expert.pyを作動させるまでのステップ(とっても簡単!)
(ターゲット環境にpythonとtfが既にインストールされているものとします)
1cd (current directory)を指定する
2cdにmnist_expert.pyとinput_data.pyを置く。
3「python mnist_expert.py」と打って、スクリプト起動させる。
コード解説
(1) ライブラリのインポート
from __future__ import absolute_import, unicode_literals
import input_data
import tensorflow as tf
import time
futureは、Python3の文法を2で使うためのライブラリです。
(2)MNISTデータ読み込み
mnist = input_data.read_data_sets(`MNIST_data/`, one_hot=True)
これのために、input_data.pyというファイルをダンロードしておく必要があります。
(3)比較対照のために、先にNNの計算をさせる
# cross_entropyを実装
sess = tf.InteractiveSession()
x = tf.placeholder(`float`, shape=[None, 784])
y_ = tf.placeholder(`float`, shape=[None, 10])
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
sess.run(tf.initialize_all_variables())
y = tf.nn.softmax(tf.matmul(x, W) + b)
cross_entropy = -tf.reduce_sum(y_ * tf.log(y))
# In this case, we ask TensorFlow to minimize cross_entropy
# using the gradient descent algorithm with a learning rate of 0.01.
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)
# 1000回学習
for i in range(1000):
batch = mnist.train.next_batch(50)
train_step.run(feed_dict={x: batch[0], y_: batch[1]})
# 結果表示
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, `float`))
print accuracy.eval(feed_dict={x: mnist.test.images, y_: mnist.test.labels})
(4) 畳込みとプーリング関数の定義
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
畳込みのpadding='SAME'は、入力と出力が同じになるように、パディングします。プーリングのPadding='SAME'は、出力が、1/2x1/2に圧縮されるように、足りないところをゼロで補完します。strides=[1, 1, 1, 1]は、1マスずつフィルタが移動するイメージ。
(5) 第一の畳込みとプーリングの演算
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
x_image = tf.reshape(x, [-1, 28, 28, 1])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
5x5サイズのフィルタを当てて、各ピクセルで32重の結果が返されるようなデザインになっています。ピクセルは、14x14に圧縮します。
(6) 第二の畳込みとプーリングの演算
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
引き続き、5x5のフィルタを当てて、畳み込みます。出力ピクセルの特徴数は64に上がる(複雑な情報の表現に向かう)。データピクセルは、7x7に圧縮。
(7) 全結合層 の演算
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
1つのピクセルに付き、1024もの情報が詰め込まれるイメージ。サイズは縮んだが、より高次の情報体になっています。
(8) Dropout
keep_prob = tf.placeholder(`float`)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
TensorFlowでは、Dropoutもシンプルな表現でできるので、便利ですね。
keep_probで元のデータの維持する比率(確率)を決めます。
(9) 読み出し層
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
ソフトマックス関数を返します。
(10) 学習方法の準備
cross_entropy = -tf.reduce_sum(y_ * tf.log(y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, `float`))
sess.run(tf.initialize_all_variables())
cross_entropyは、交差エントロピー誤差関数です。y_は、教師データの符号データです。
train_stepは、Adamという手法で勾配計算しています。(学習係数のコントロールもこれ)
精度(正解率)の定義、および変数の初期化が続きます。
(11) 学習の実行
for i in range(20000):
batch = mnist.train.next_batch(50)
if i % 100 == 0:
train_accuracy = accuracy.eval(feed_dict={ x: batch[0], y_: batch[1], keep_prob: 1.0})
print `step %d, training accuracy %g` % (i, train_accuracy)
print('elapsed_time: %.3f [sec]' % (time.time()-start))
print('100steps time: %.3f [sec]' % (time.time()-present))
present = time.time() train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
メイン計算は、
batch = mnist.train.next_batch(50)
の1行でできています。ホント便利。
この部分における殆どの命令が、精度の出力に関する記述です。
(12) テストデータとの比較
print `test accuracy %g` % accuracy.eval(feed_dict={
x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}) init = tf.initialize_all_variables() best_loss = float(`inf`)
動作結果
メモリ2GBのVirtual Mediaで動かしていたのですが、メモリ不足のため、テストデータの確認ができなかった。
(マシンスペックではCPU/GPUの計算速度の話題が典型ですが、それ以前のスペックで恐縮です汗)
訓練データの学習は、よく進みました。
100ステップで約43秒、20000ステップで2時間弱という負荷でした。
コマンドラインのイメージ↓



0 件のコメント:
コメントを投稿