为了寻求最优解,在低维的时候,正规方程组是最直接的方式。因为它要计算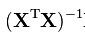 ,其复杂度为
,其复杂度为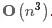 。如图1,m代表样例,n代表特征
。如图1,m代表样例,n代表特征
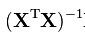 ,其复杂度为
,其复杂度为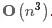 。如图1,m代表样例,n代表特征
。如图1,m代表样例,n代表特征
图1
图1中,矩阵X记录了特征值,向量y是实际的数据。要使h(x)与y的偏差最小,将要计算
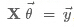
就将问题转化为正规方程组,这种解决方式被称为“inconsistent”,下面给出证明:

更直观的图表解释:
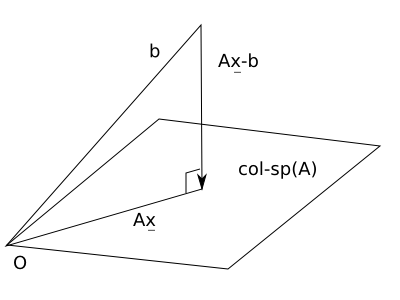
当矩阵A的宽度小于它的高度时, A x = b 的解可用: 满足 A' (A x - b) = 0 的 x 来近似。
A x 的几何意义: 当 x 自由变动, A x 产生 A 的 column space。
A x = b 想要有解, b 必须落在 A x 的 column space 当中。
b 若不落在 A x 的 column space 当中, 只好退而求其次: 至少 b 的 投影projection 必然落在此空间当中 (by definition)。
试图寻找 x 使得 A x - b 的长度 (也就是误差值) 最小。
上述误差的最小值正好发生在误差向量与 A 的 columnspace 垂直时, 也就是说, 希望误差向量落在 A' 的 null space
上图中的 A 是一个 3x2 的矩阵; 图中的四边形标示出 A 的column space 那个平面; 而 b 则是那个平面之外的一点。 x 是 Ax = b 的最佳近似解
梯度下降和正规方程组的对比:

0 件のコメント:
コメントを投稿